Home ≫ Arithmetic Aptitute ≫ Elementary Mensuration-I ≫ Page 12
111. There is an equilateral triangle of which each side is 2 m. With all the three corners as centres, circles are described each of radius 1m.
(i) Calculate the area common to all the circles and the triangle.
(ii) Find the area of the remaining portion of the triangle.
  A.  Area common: 1.63 sq m; Area of remaining portion: 0.142 sq m
  B.  Area common: 1.29 sq m; Area of remaining portion: 0.184 sq m
  C.  Area common: 1.48 sq m; Area of remaining portion: 0.212 sq m
  D.  Area common: 1.57 sq m; Area of remaining portion: 0.162 sq m
     
   
View Answer

Shortcut:
There is an equilateral triangle of which each side is 'z' metres. With all the three corners as centres, circles are described each of radius
z / 2
metres. The area common to all the circles and the triangle is
1 / 8
πz2 or
1 / 2
π(radius)2 and the area of the remaining portion(shaded portion) of the triangle is √3 −
π / 2
x (radius)2 or (0.162)(radius)2 or, (0.0405)z2

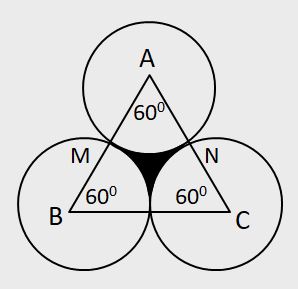
Here, z = 2, r = 1
When the side of the equilateral triangle is double the radius of the circles, all circles touch each other and in such cases the following formula may be used:
Area of each sector =
1 / 6
x π x (radius)2
Area of remaining (shaded) portion = √3 −
π / 2
x (radius)2
In this question, the area common to all circles and triangle = sum of the area of three sectors AMN, BML and CLN =
1 / 6
x π x (r)2 +
1 / 6
x π x (r)2+
1 / 6
x π x (r)2 =
1 / 2
x π x (r)2
=
1 / 2
x
22 / 7
x (1)2 = 1.57 sq m.
(ii) The area of the remaining portion of the triangle = The area of the shaded portion = 0.162 x (1)2 = 0.162 sq m.

112. The diameter of a coin is 1 cm. If four to these coins be placed on a table so that the rim of each touches that of the other two, find the area of the unoccupied space between them.
  A.  Area of unoccupied space: 0.155 sq cm
  B.  Area of unoccupied space: 0.215 sq cm
  C.  Area of unoccupied space: 0.515 sq cm
  D.  Area of unoccupied space: 0.805 sq cm
     
   
View Answer

Shortcut:
The diameter of a coin is 'z' cm If four of these coins be placed on a table so that the rim of each touches that of the other two, then the area of the unoccupied space between them is
4 − π / 4
x z2 or,
3 / 14
x z2 or (0.215)(z)2 sq cm and area of each sector is given by
1 / 16
x π x (z)2 sq cm

Here, If the circles be placed in such a way that they touch each other, then the square's side is double the radius. In such cases the following formulae may be used:
Area of each sector =
1 / 4
x π x (radius)2
=
1 / 4
x π x (z)2
Area of remaining (shaded) portion = (4 − π)(radius)2
4 − π / 4
x (z)2 = (0.86)(radius)2
Now, in this question, the area of unoccupied space = (0.86)(radius)2
= (0.86)
(
1 / 2
)
2 = 0.215 sq cm

113. The length of a rectangle is increased by 60%. By what per cent should the width be decreased to maintain the same area?
  A.  39
3 / 5
%
  B.  31
4 / 9
2%
  C.  37
1 / 2
%
  D.  33
3 / 2
%
     
   
View Answer

Shortcut:
If the length of a rectangle is increased by a%, then the percentage decrease in width, to maintain th same area, is given by
a / 100 + a
x 100
Here, a = 60
Required percentage decrease in breadth =
60 / 100 + 60
x 100
=
60 / 160
x 100
=
75 / 2
= 37
1 / 2
%.

114. The length of a rectangle is increased by 20%. By what percent should the width be decreased so that area of the rectangle decreases by 20%?
  A.  37
1 / 4
%
  B.  39
5 / 4
%
  C.  33
1 / 3
%
  D.  27
2 / 3
%
     
   
View Answer

Shortcut:
If the length of a rectangle is increased by a%, then the percentage decrease in width, to reduce the area by b%, is given by
a + b / 100 + a
x 100
Here, a = 20, b = 20
Required percentage =
60 + 20 / 100 + 20
x 100
=
80 / 120
x 100
=
100 / 3
= 33
1 / 3
%.

115. The length of a rectangle is increased by 20%. By what per cent should the width be decreased so that area of the rectangle increases only by 4%.
  A.  13
1 / 3
%
  B.  11
2 / 3
%
  C.  15
5 / 7
%
  D.  9
1 / 3
%
     
   
View Answer

Shortcut:
If the length of a rectangle is increased by a%, then the percentage decrease in width, to increase the area by b%, is given by
Difference in a and b / 100 + a
x 100
Here, a = 20, b = 4
Required percentage =
20 − 4 / 100 + 20
x 100
=
16 / 120
x 100
=
40 / 3
= 13
1 / 3
%.

116. The length of a rectangle is decreased by 20%. By what percent should the width be increased, so that area of the rectangle increases by 20%?
  A.  40%
  B.  25%
  C.  20%
  D.  50%
     
   
View Answer

Shortcut:
If the length of a rectangle is decreased by a%, then the percentage increase in width, to increase the area by b%, is given by
a + b / 100 − a
x 100
Here, a = 20, b = 20
Required percentage =
20 + 20 / 100 − 20
x 100
=
40 / 80
x 100 = 50%.

117. If the length of a rectangle is decreased by 20%, by what per cent should the width be increases to maintain the same area?
  A.  25%
  B.  15%
  C.  30%
  D.  40%
     
   
View Answer

Shortcut:
If the length of a rectangle is decreased by a%, then the percentage increase in width, to maintain the same area, is given by
a / 100 − a
x 100
Here, a = 20
Required percentage increase in breadth =
20 / 100 − 20
x 100
=
20 / 80
x 100 = 25%.

118. If the length and the breadth of a rectangle is increased by 5% and 4% respectively, then by what per cent does the area of that rectangle increase?
  A.  9.2%
  B.  8.6%
  C.  10 %
  D.  12%
     
   
View Answer

Shortcut:
If length and breadth of a rectangle is increased a% and b% respectiely, then area is increased by
(
a + b +
ab / 100
)
%
Here, a = 5, b = 4
Required percentage =
(
5 + 4 +
5 x 4 / 100
)
%
= 9 +
20 / 100
= 9 + 0.2 = 9.2%

119. If the length of a rectangle increase by 10% and the breadth of that rectangle decreases by 12%, then find the percent change in area.
  A.  2.5 % decrease
  B.  3.2 % decrease
  C.  3.5 % decrease
  D.  4 % decrease
     
   
View Answer

Shortcut:
If length and breadth of a rectangle is increased a% and b% respectively, then area is increased by
(
a + b +
ab / 100
)
%
Here, a = 10, b = −12
Required percentage =
[
10 + (−12) +
10 x (−12) / 100
]
%
=
(
−2 −
120 / 100
)
% = −2 −1.2 = −3.2%
Hence, the area will decrease by 3.2%.

120. The length of a square is increased by 40% while breadth is decreased by 40%. The ratio of area of the resulting rectangle so formed to that of the original square is:
  A.  22 : 21
  B.  19 : 24
  C.  23 : 28
  D.  21 : 25
     
   
View Answer

Shortcut:
If length and breadth of a rectangle is increased a% and b% respectively, then area is increased by
(
a + b +
ab / 100
)
%
Here, a = 40, b = −40
Required percentage =
{
40 + (−40) +
40 x (−40) / 100
}
%
= −
1600 / 100
% = −16%
∴ the area will decrease by 16%.
Required ratio =
100 − 16 / 100
=
84 / 100
= 21 : 25

Copyright © 2020-2022. All rights reserved. Designed, Developed and content provided by Anjula Graphics & Web Desigining .