Home ≫ Arithmetic Aptitute ≫ Elementary Mensuration-I ≫ Page 14
131. Two poles 15 m and 30 m high stand upright in a playground. If their feet be 36 m apart, find the distance between their tops.
  A.  39 cm
  B.  27 cm
  C.  33 cm
  D.  42 cm
     
   
View Answer

Shortcut:
Two poles 'a' meter and 'b' meter high stand upright. If there feet be 'c' meter apart, then the distance between their tops is √[c2 + (b − a)2] metres.

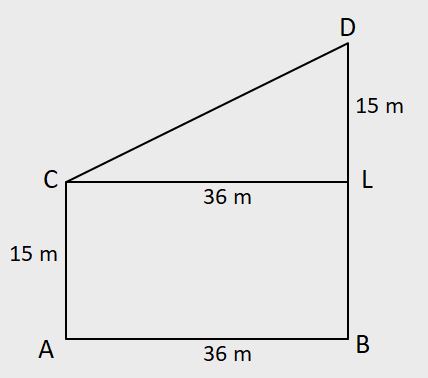
Here, a = 15, b = 30, c = 36
Using these values in the shortcut, we get:
The distance between their tops = √[362 + (30 − 15)2]
= √[362 + (15)2]
= √[1296 + 225] = √(1521) = 39
Hence, the distnace between their tops is 39 metres.

132. The circumference of a circle is 100 cm. Find the side of the square inscribed in the circle.
  A.  √3 x 40/π
  B.  √2 x 50/π
  C.  √5 x 30/π
  D.  √6 x 25/π
     
   
View Answer

Shortcut:
Area of a square inscribed in a circle o radius r is 2r2 and side of a square inscribed in a circle of radius r is √(2)r
Here, 2πr = 100
r =
50 / π

Using this value in the shortcut, we get:
Side of square inscribed = √(2) x
50 / π

=
√2 x 50 / π

133. The largest triangle is inscribed in a semi-circle of radius 14 cm. Find the area of the triangle.
  A.  200 sq cm
  B.  196 sq cm
  C.  192 sq cm
  D.  195 sq cm
     
   
View Answer

Shortcut:
The area of the largest triangle inscribed in a semi-circle of radius r is r2
Here, r = 14
Using this value in the shortcut, we get:
Required area = (14)2 = 196
Hence, the area of the triangle is 196 sq cm.

134. The largest triangle is inscribed in a semi-circle of radius 14 cm. Find the area inside the semi-circle which is not occupied by the triangle.
  A.  112 sq cm
  B.  105 sq cm
  C.  113 sq cm
  D.  115 sq cm
     
   
View Answer

Shortcut:
If the largest triangle is inscribed in a semi-circle of radius 'r' cm, then the area inside the semi-circle which is not occupied by the triangle is
4 / 7
x r2 sq cm
Here, r = 14
Using this value in the shortcut, we get:
Required area =
4 / 7
x (14)2
=
4 / 7
x 14 x 14 = 4 x 2 x 14 = 112
Hence, the area is 112 sq cm.

135. Find the area of the largest circle that can be drawn in a square of side 14 cm.
  A.  158 cm 2
  B.  154 cm 2
  C.  155 cm 2
  D.  150 cm 2
     
   
View Answer

Shortcut:
The area of the largest circle that can be drawn in a square of side 'a' is π x
(
a / 2
)
2
Here, a = 14
Using this value in the shortcut, we get:
Required area = π x
(
14 / 2
)
2
=
22 x 14 x 14 / 7 x 2 x 2
= 22 x 7 = 154
Hence, the area is 154 sq cm.

136. In a quadrilateral, the length of one of its diagonals is 23 cm and the perpendiculars drawn on this diagonal from other two vertices measure 17 cm and 7 cm respectively. Find the area of the quadrilateral.
  A.  276 sq cm
  B.  265 sq cm
  C.  270 sq cm
  D.  280 sq cm
     
   
View Answer

Shortcut:
To find the area of the quadrilateral when its any diagonal (D) and the perpendiculars (P1 & P2) drawn on this diagonal from other two vertices are given.
Area of the quadrilateral =
1 / 2
x any diagonal x (sum of perpendiculars drawn on diagonal from two vertices)
or
=
1 / 2
x D x (P1 + P2)
Here, D = 23, P1 = 17, P2 = 7
Using these values in the shortcut, we get:
Required area =
1 / 2
x 23 x (17 + 7)
=
1 / 2
x 23 x 24 = 23 x 12 = 276
Hence, the area is 276 sq cm.

137. The side of an equilateral triangle is 9 cm long. Find the area of the circle circumscribing the equilateral triangle.
  A.  30π sq cm
  B.  21π sq cm
  C.  25π sq cm
  D.  27π sq cm
     
   
View Answer

Shortcut:
The area of a circle circumscribing an equilateral triangle of side 'a' is
π / 3
x (a)2

Here, a = 9
Using these values in the shortcut, we get:
Required area =
π / 3
x (9)2
=
π / 3
x 9 x 9 = π x 3 x 9 = 27π
Hence, the area is 27π sq cm.

138. The length of side of an equilateral triangle is 9 cm. Find the area of the circle inscribing the equilateral triangle.
  A.  
28π / 5
sq cm
  B.  
25π / 3
sq cm
  C.  
27π / 4
sq cm
  D.  
27π / 2
sq cm
     
   
View Answer

Shortcut:
The area of a circle inscribed in an equilateral triangle of side 'a' is
π / 12
x (a)2

Here, a = 9
Using these values in the shortcut, we get:
Required area =
π / 12
x (9)2
=
π / 12
x 9 x 9
=
27π / 4

Hence, the area is
27π / 4
sq cm.

139. There is an equilateral triangle of side 12 cm. Find the radius of the circle that can be drawn in the equilateral triangle.
  A.  5√3 cm
  B.  2√3 cm
  C.  2√5 cm
  D.  3√2 cm
     
   
View Answer

Shortcut:
Radius of a largest circle that can be drawn in an equilateral triangle of side 'a' units is
(
√3 / 6
x a
)
units.
Here, a = 12
Using these values in the shortcut, we get:
Required area =
(
√3 / 6
x 12
)
= 2√3
Hence, the area is 2√3 sq cm.

140. The length of side of an equilateral triangle is 10 cm. Find the ratio of the areas of the circle circumscribing the triangle to the circle inscribing the triangle.
  A.  4 : 1
  B.  2 : 1
  C.  3 : 4
  D.  1 : 4
     
   
View Answer

Shortcut:
An equilateral triangle is circumscribed by a circle and another circle is inscribed in that triangle then the ratio of the areas of the two circles is 4 : 1.

Here, using the above shortcut, we get:
Required ratio = 4 : 1.

Copyright © 2020-2022. All rights reserved. Designed, Developed and content provided by Anjula Graphics & Web Desigining .