|
A man wishes to find the height of a flagspost which stands on a horizontal plane, at a point on this plane he finds the angle of elevation of the top of the flagspost to be θ1. On walking 'z' units towards the tower he finds the corresponding angle of elevation to be θ2. Then the height (H) of the flagpost is given by
[
ztanθ1tanθ2
/
tanθ2 − tanθ1
] units and the value of DB(below given) is given by
ztanθ1
/
tanθ2 − tanθ1
units.
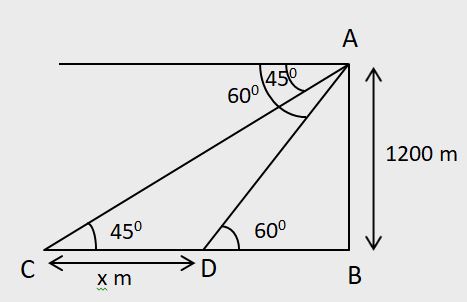
z = ?
θ1 = 45°
θ2 = 60°
Height = 1200
Using these values in the shortcut, we get:
1200 =
z x tan60° x tan45°
/
tan60° − tan45°
z = 1200[
tan60° − tan45°
/
tan60° x tan45°
]
z = 1200[
√3 − 1
/
√3 x 1
]
z = 1200[
√3 − 1
/
√3
]
z = 1200[ 1 −
1
/
√3
]
z = 1200 −
1200 x √3
/
√3 x √3
z = 1200 −1200(
√3
/
3
)
z = 1200 − 400√3
z = [1200 − (400 x 1.732)] = 507.2
Hence, the distance between the two ships is 507.2 metres.
|