Shortcut:
From the top and bottom of a building of height 'm' units, the angles of elevation of the top of a tower are θ1 and θ2 respectively, then the,
(i) Height of the tower =
mtanθ2
/
tanθ2 − tanθ1
units,
(ii) Distance between the building and the tower =
m
/
tanθ2 − tanθ1
units
(iii) RM(See the below figure) =
mtanθ1
/
tanθ2 − tanθ1
units
[Note: If height of the tower is 'H' units, then the distance between the building and the tower is
H
/
tanθ2
units.]
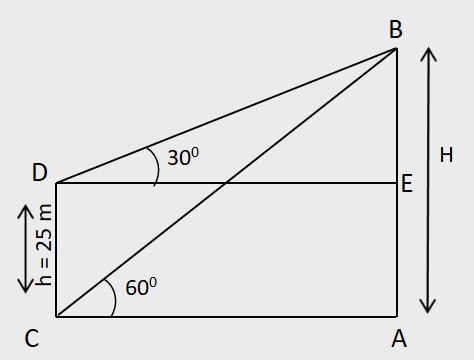
Here, m = 25, θ1 = 30°, θ2 = 60°
Using these values in the shortcut, we get:
Height of tower =
25 x tan60°
/
tan60° − tan30°
=
25 x √3
/
√3 − 1/√3
=
25 x √3 x √3
/
(√3 x √3 − 1)
=
25 x 3
/
(3 − 1)
=
25 x 3
/
2
= 37.5
Hence, the height of the column is 37.5 metres.
|