Shortcut:
The angles of depression of two ships from the top of a lighthouse are θ1 and θ2. If the ships are 'm' metres apart, then the,
(i) Height of the lighthouse =
mtanθ1tanθ2
/
tanθ1 + tanθ2
metres,
(ii) Distance of ship at P from the foot of the lighthouse =
mtanθ1
/
tanθ1 + tanθ2
metres
(iii) Distance of ship at Q from the foot of lighthouse =
mtanθ2
/
tanθ1 + tanθ2
metres
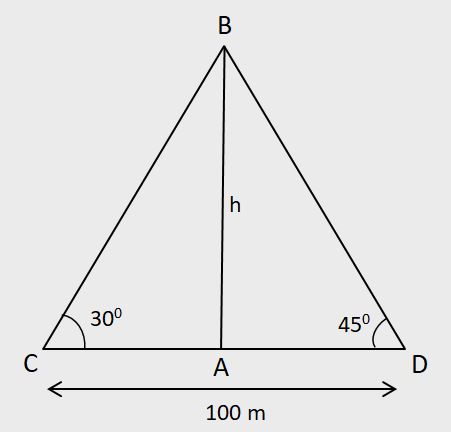
Here, m = 100, θ1 = 30°, θ2 = 45°
Using these values in the shortcut, we get:
Height of tower =
100 x tan30° x tan45°
/
tan30° + tan45°
=
100 x tan30° x tan45°
/
tan30° + tan45°
=
100 x 1/√3 x 1
/
1/√3 + 1
=
100 x 1 x 1
/
1 + √3
=
100
/
1 + 1.732
=
100
/
2.732
= 36.6
Hence, the height of the house is 36.6 metres.
|