Shortcut:
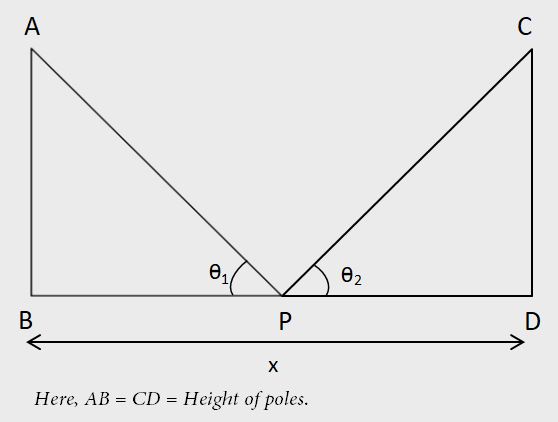
Two poles of equal heights stand on either sides of a roadway which is 'z' units wide. At a point of the roadway between the poles, the elevations of the tops of the pole are θ1° and θ2°, then the
(i) the heights of poles =
ztanθ1tanθ2
/
tanθ1 + tanθ2
units and the
(ii) position of the point P from B(see the figure) =
ztanθ2
/
tanθ1 + tanθ2
units.
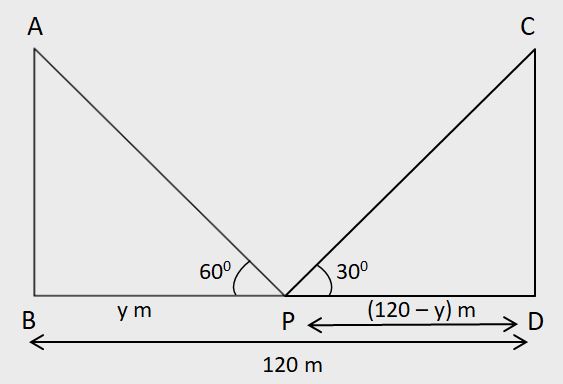
Here, θ1 = 60°, z = 120, θ2 = 30°
Using these values in the shortcut, we get:
Height of the pole =
120 x √3 x 1/√3
/
√3 + 1/√3
= 30√3
Hence, the height of the pole is 30√3 metres.
(ii) Position of the point P from B =
120 x 1/√3
/
√3 + 1/√3
= 30
Hence, the position of the point P from B is 30 metres.
|